We’ve all, more or less, heard of or experienced the so-called six degrees of separation. The theory, which is attributed to Harvard professor Stanley Milgram’s experiment, demonstrates that we live in a small world where, more often than not, we are only six steps away from connecting with anyone. Move interconnectivity to the web, you’ll find that “any document is on average only nineteen clicks away from any other,” writes Albert-László Barabási in his book, Linked.

But our idea of the Web, with search engines like Google connecting us to webpages, which then direct us to other hyperlinks — this interconnected world, how does it all begin?

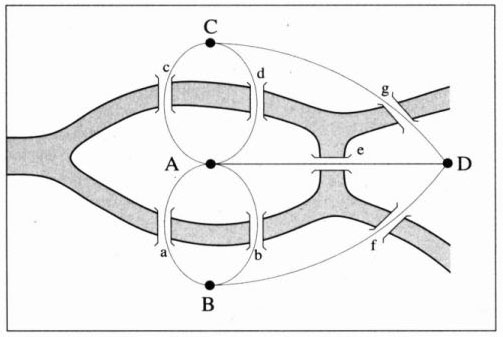
The book, explores the problem with a famous mathematical problem, the Königsberg Bridge problem. In Königsberg, Russia, there are seven bridges connecting the city to the island of Kneiphof. The puzzle asks:

 Can one walk across the seven bridges and never cross the same one twice?

Well, I would have to see the location of the bridges.

Fair enough.

Konigsberg Bridge Puzzle (image credit: simonkneebone)

And then, and then… I would try walking through all my solutions? 

The puzzle was solved by Leonhard Euler, a Swiss-born mathematician who broke the problem into four “nodes” and seven “links” (aka bridges), and thus proved that the path — to walk all seven bridges once, and once only — does not exist.

(image credit: Weber Edu/ Albert-László Barabási)

You’ve got nodes, links and paths. And with randomness thrown into network theory, voilà, the Web.

In consideration of the likelihood of me knowing, well you, eventually by however many degrees of separation, I would say, that photo from last night is best keep private.